The Banach-Tarski Paradox

Given a solid ball in 3‑dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball.The reassembly process involves only moving the pieces around and rotating them without changing their shape.

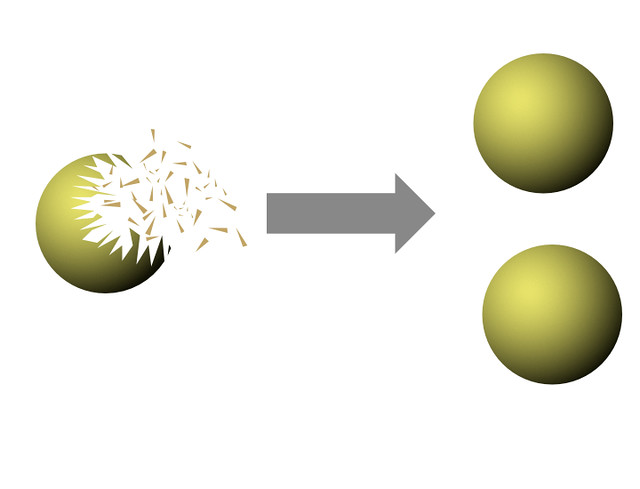
The Banach-Tarski Paradox

This ‘paradox’ is a firm result in set theory. It’s not up for debate.

Now, as you might have guessed, there is a wrinkle. That is, the individual pieces - the ‘disjoint subsets’ - aren’t ordinary solid pieces: each piece is an infinite scattering of points. This is where the usual concept of volume being preserved runs into a difficulty.

Nevertheless I’m continuing my researches into this using a small sphere made of gold. A stronger form of the theorem, you see, is that any sphere can be cut into pieces and reassembled into any other sphere of any volume. It’s often stated as, ‘a pea can be chopped up and reassembled into the Sun’. Or…a gold ball can be chooped up and reassembled into another gold ball of any desired size…

The Banach-Tarski Paradox